Problémy založené na
splňování podmínek (Constraint Satisfaction Problems) představují častou
reprezentaci praktických problémů (třeba rozvrhovacích). Jednoduchým příkladem
je Sudoku - rozvrhnout čísla tak, aby splňovala podmínky. Popis problému
obsahuje:
- proměnné s jejich doménami = povolenými hodnotami; (Sudoku: každé políčko =
proměnná, domény jsou {1,2,...,9})
- množina podmínek na těchto proměnných; (Sudoku: proměnné v každém
čtverci 3x3, v každém sloupci a v každém řádku musejí mít různé
hodnoty).
Úkolem je najít ohodnocení proměnných splňující
všechny podmínky, někdy se také optimalizuje hodnotící funkce (mohou existovat
"lepší" a "horší" řešení).
Na rozdíl od
klasického prohledávání stavového prostoru, kde je důležitá cena cesty
do koncového stavu, v tomto případě na délce cesty k řešení nezáleží
(většinou jsou stejné), ale rozhodující je najít řešení samotné a
přitom prohledat co nejméně stavů. Soustava podmínek umožňuje často výrazně
omezit prohledávanou část stavového prostoru. Omezující podmínky určují graf
závislosti jednotlivých proměnných (např. u Sudoku jsou vzájemně
závislé proměnné v každém čtverci, pak v každém sloupci a v každém
řádku.
Příklad podmínek pro problém N dam
Rozmístěte N dam na
šachovnici N x N, aby se vzájemně neohrožovaly (viz prezentace Illinois):
Proměnné:
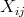 ,1≤ i,j ≤N
,1≤ i,j ≤N
Domény: 0,1
Význam:
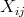 =1→ na políčku se
souřadnicemi (i,j) je dáma,
=1→ na políčku se
souřadnicemi (i,j) je dáma,
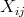 =0 → na políčku
není dáma
=0 → na políčku
není dáma
Podmínky:
 = N Počet
dam, tj. políček s
= N Počet
dam, tj. políček s
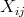 =1 na šachovnici musí
být N
=1 na šachovnici musí
být N
∀ i,j,k, j ≠ k: (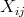 ,
, 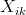 ) ∈ {(0,0),(0,1),(1,0)} Na žádné
dvojici políček se souřadnicemi (i,j) a (i,k), tj. ležících v
jednom řádku, nejsou dvě dámy, čili dvojice hodnot (1,1)
) ∈ {(0,0),(0,1),(1,0)} Na žádné
dvojici políček se souřadnicemi (i,j) a (i,k), tj. ležících v
jednom řádku, nejsou dvě dámy, čili dvojice hodnot (1,1)
∀ i,j,k, i ≠ k: (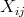 ,
, 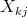 ) ∈ {(0,0),(0,1),(1,0)} V žádném sloupci nejsou dvě dámy
) ∈ {(0,0),(0,1),(1,0)} V žádném sloupci nejsou dvě dámy
∀ i,j,k, 1 ≤ k ≤ N−1: (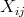 ,
, 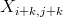 ) ∈ {(0,0), (0,1), (1,0)}
Na žádné diagonále
rovnoběžné s hlavní diagonálou nejsou dvě dámy
) ∈ {(0,0), (0,1), (1,0)}
Na žádné diagonále
rovnoběžné s hlavní diagonálou nejsou dvě dámy
∀ i,j,k, 1 ≤ k ≤ N−1:
(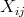 ,
, 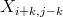 ) ∈ {(0,0), (0,1), (1,0)} Na žádné diagonále
rovnoběžné s vedlejší diagonálou nejsou dvě dámy
) ∈ {(0,0), (0,1), (1,0)} Na žádné diagonále
rovnoběžné s vedlejší diagonálou nejsou dvě dámy
Postup řešení:
Prohledávání stavového
prostoru, kde každý stav je (částečné) ohodnocení proměnných. Akce (přechod
mezi stavy) je ohodnocení jedné prázdné proměnné tak, že neporuší žádnou
podmínku. Cílový stav = úplné přiřazení proměnných.
Pak víme, že při n proměnných
se řešení nachází vždy v hloubce n prohledávacího stromu, a
navíc nezáleží na pořadí přiřazení do proměnných. Lze tedy použít jednoduché
prohledávání do hloubky s návratem (Backtracking search) - víme, že
hloubky stromu je vždy omezená. Je to ale neinformovaná a neefektivní metoda.
Informované metody - vyšší efektivita prohledávání:
- Nejprve ohodnocovat nejvíce omezenou proměnnou, tedy tu s
nejmenším počtem zbývajících přípustných hodnot. V případě rovnosti se volí
proměnná svázaná nejvíce podmínkami s doposud neohodnocenými proměnnými.
- Vybírat k přiřazení hodnoty, které nejspíše patří do řešení, například
ty, které nejméně omezují ostatní doposud neohodnocené proměnné. Určení
takových hodnot závisí na konkrétním problému.
- Dopředná kontrola – při přiřazení hodnoty se
podíváme na podmínky dalších proměnných spojené s přiřazenou proměnnou, a
odstraníme jejich hodnoty, které podmínky nesplňují.
- Konzistence podmínek – pokud se odfiltrují některé
nepřípustné hodnoty z domén, lze pomocí grafu závislosti omezit i hodnoty
dalších proměnných, a tím zmenšit prohledávanou část stavového prostoru.
- V případě grafu závislosti proměnných bez cyklů existuje
rychlý algoritmus, který vždy najde řešení; dá se použít i tehdy, pokud je
cyklů jen málo a přiřazením některých proměnných se dají cykly odstranit.
Cíle
Klíčová slova