Týden 9
Cykly
Cyklus slouží pro zápis příkazů, které mají být prováděny opakovaně (několikrát za sebou). Počet opakování těchto příkazů závisí na nějaké podmínce nebo může být předem známý. Proto existují dva základní typy cyklů:
- cyklus řízený podmínkou (zvaný též indukční cyklus; v MATLABu realizovaný pomocí
while) - cyklus s předem známým počtem opakování (zvaný též iterační cyklus nebo cyklus s výčtem hodnot; v MATLABu realizovaný pomocí
for)
Příkazy uvnitř cyklu se nazývají tělo cyklu.
Cyklus řízený podmínkou - while
Cyklus řízený podmínkou používáme, pokud chceme několikrát provést určité příkazy, ale předem neznáme počet opakování, nicméně známe podmínky, za kterých se příkazy provádět mají. Tato podmínka se nazývá řídící podmínka cyklu. V MATLABu je tento druh cyklu realizován příkazem while.
Syntaxe
Cyklus while začíná klíčovým slovem while a končí klíčovým slovem end:
while podmínka příkazy end
podmínka(řídicí podmínka cyklu) je libovolný výraz s logickou hodnotou 0 nebo 1 (většinou se v podmínkách používají relační nebo binární logické operátory)příkazyv těle cyklu jsou jakékoli příkazy, které se mají provádět opakovaně v případě splnění podmínky
Poznámky:
- V případě, že součástí podmínky je matice typu mxn, je podmínka pravdivá jen tehdy, pokud je pravdivá pro všechny prvky této matice.
- V případě, že v nějaké podmínce použijeme binární logický operátor (& nebo |) a po vyhodnocení prvního argumentu je už zřejmý výsledek (kdy se to může stát?), tak se druhý argument nevyhodnocuje. Tato vlastnost se nazývá zkrácené vyhodnocování.
- Cyklus
whilemůže být vnořen do libovolného jiného složeného příkazu (např. doifu nebo do jiného cyklu). - Mezi příkazy těla cyklu můžeme napsat jakýkoli jiný složený příkaz, např.
ifnebo další cyklus.
Činnost (průběh provádění cyklu)
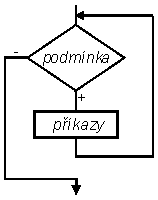 Činnost cyklu lze vyjádřit větou: dokud platí podmínka, prováděj příkazy.
Činnost cyklu lze vyjádřit větou: dokud platí podmínka, prováděj příkazy.
Na začátku se testuje platnost řídicí podmínky (tj. je vyhodnocena). Pokud podmínka platí (tj. výraz má nenulovou hodnotu), provedou se všechny příkazy těla cyklu. Poté se ZNOVU testuje podmínka a pokud platí, provedou se znovu všechny příkazy těla cyklu atd. atd., dokud se při testování podmínky nezjistí, že podmínka neplatí (tj. hodnota výrazu je nulová). Tehdy cyklus skončí, tzn. pokračuje se prováděním příkazů za jeho koncem (který je označen klíčovým slovem end), pokud tam nějaké jsou.
Konec cyklu může nastat i při prvním testu podmínky (je-li nulová), takže se může stát, že příkazy v těle cyklu se neprovedou ani jednou.
Protože se podmínka testuje opakovaně a závisí na ní ukončení cyklu, měli bychom dodržovat následující doporučení:
řídicí podmínka cyklu by měla být ovlivňována prováděním příkazů v těle cyklu tak, aby jednou přestala platit. Jinak totiž cyklus nikdy neskončí (tzv. nekonečný cyklus) - poznáme to tím, že v Command Window se neobjeví >> a zpravidla se také neustále něco vypisuje. Pokud chceme ukončit provádění nekonečného cyklu, stiskneme CTRL+C.
Příklad nekonečného cyklu:
while 1 % podmínka je vždy pravdivá, má totiž pořád hodnotu 1
disp('jedu...')
end
Použití cyklu řízeného podmínkou
Cyklus while používáme vždy, když potřebujeme opakovat nějakou činnost závislou na pravdivosti dané podmínky, ale předem neznáme počet těchto opakování.
Příklad 1 - vytvoříme funkci, která počítá zbytek po dělení a celočíselný podíl ze dvou zadaných čísel:
| deleni.m |
function [p,z]=deleni(d1,d2) % DELENI - celociselny podil a zbytek po deleni % d1 ... delenec (cele cislo) % d2 ... delitel (cele cislo) % p ... celociselny podil % z ... zbytek po delenip = 0; % priprava podilu while d1>=d2 % dokud je delenec vetsi nebo roven deliteli d1 = d1-d2; % nicime puvodni delenec postupnym odecitanim delitele, tj. d1-d2-d2-d2... p = p+1; % hlidame si pocet odecteni, tj. postupne nam narusta podil end z = d1; % nakonec nam z delence zustala pouze cast mensi nez delitel (zbytek) |
Všimněte si, že funkce nic NEVYPISUJE, pouze vyrobí výstupy ze zadaných vstupů.
Na první pohled bude funkce fungovat správně: vyzkoušejme ji např. pro 10 a 3, 25 a 25, 17 a 21 nebo 0 a 6 (doporučení: chcete-li činnost funkce prozkoumat, v některém případě i krokujte - breakpoint nastavte třeba na řádek p=0;):>> [podil,zbytek]=deleni(10,3)
>> [podil,zbytek]=deleni(25,25)
>> [podil,zbytek]=deleni(17,21)
>> [podil,zbytek]=deleni(0,6)
Když ale zadáme třeba 5 a 0 nebo 6 a -3 (>> [podil,zbytek]=deleni(6,-3)), tak cyklus nikdy neskončí, protože d1 v podmínce stále narůstá!
Vylepšíme tedy naši funkci o test nezápornosti dělitele (a test kladnosti dělence):
| deleni.m |
function [p,z]=deleni(d1,d2)
% DELENI - celociselny podil a zbytek po deleni
% [p,z]=deleni(d1,d2)
% d1 ... delenec (cele cislo)
% d2 ... delitel (cele cislo)
% p ... celociselny podil
% z ... zbytek po deleniif d1<0 | d2<=0 % delenec je zaporny nebo delitel je nula ci zaporny
error('chybne zadane vstupy') % KONEC, nic nepocitame
end
p = 0; % priprava podilu
while d1>=d2 % dokud je delenec vetsi nebo roven deliteli
d1 = d1-d2; % nicime puvodni delenec postupnym odecitanim delitele, tj. d1-d2-d2-d2...
p = p+1; % hlidame si pocet odecteni, tj. postupne nam narusta podil
end
z = d1; % nakonec nam z delence zustala pouze cast mensi nez delitel (zbytek)
|
Příklad 2 - funkce pro výpočet faktoriálu zadaného čísla (na principu: n!=n(n-1)(n-2)...1):
| fakt1.m |
function f=fakt1(n)
% FAKT1 - vypocet faktorialu celeho cisla
% f=fakt1(n)
% n ... cislo
% f ... faktorial (f=n!)if n<0 % kontrola vstupu
error('faktorial neexistuje') % KONEC, nic nepocitame
end
f = 1; % priprava vysledku
while n>1 % dokud je co pridat do vysledku
f = f*n; % pridavame do vysledku
n = n-1; % postupne snizujeme 'n'
end
% nakonec je 'n' rovno jedne a 'f' obsahuje jeho faktorial
|
Cyklus s předem známým počtem opakování (iterační cyklus) - for
Tento cyklus používáme, když předem víme, kolikrát se mají provést určité příkazy. Počet opakování je většinou daný vektorem, ze kterého si v každé iteraci (tj. v každém průchodu cyklem) vezmeme jednu hodnotu - tato hodnota je uložena v tzv. řídicí proměnné cyklu. V MATLABu je tento druh cyklu realizován příkazem for.
Syntaxe
Cyklus for začíná klíčovým slovem for a končí klíčovým slovem end:
for proměnná=výraz příkazy end
proměnná(řídicí proměnná cyklu) je libovolný název proměnnévýrazje jakýkoli výraz, jehož délka (velikost) udává počet opakování. Většinou se jedná o vektor, který bývá generován pomocí operátoru dvojtečkapříkazyv těle cyklu jsou jakékoli příkazy, které se mají provádět opakovaně v případě splnění podmínky
Poznámky:
- V případě, že výsledkem výrazu (nebo výrazem samotným) je matice, bude řídicí proměnná obsahovat postupně každý její sloupec.
- Cyklus
formůže být vnořen do libovolného jiného složeného příkazu (např. doifu nebo do jiného cyklu). - Mezi příkazy těla cyklu můžeme napsat jakýkoli jiný složený příkaz, např.
ifnebo další cyklus.
Činnost (průběh provádění cyklu)
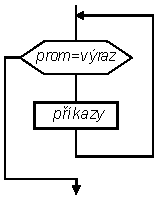 Činnost cyklu lze vyjádřit větou: n-krát proveď příkazy (n je délka výrazu, tj. počet prvků vektoru nebo počet sloupců matice).
Činnost cyklu lze vyjádřit větou: n-krát proveď příkazy (n je délka výrazu, tj. počet prvků vektoru nebo počet sloupců matice).
Na začátku se zjistí délka (n) výrazu a pokud je nenulová, n-krát se provede tělo cyklu (příkazy). V každé iteraci je řídicí proměnná cyklu rovna jednomu prvku vektoru (začíná se prvním prvkem a pokračuje se po řadě). Po vyčerpání všech hodnot vektoru cyklus skončí, tzn. pokračuje se prováděním příkazů za jeho koncem (který je označen klíčovým slovem end), pokud tam nějaké jsou.
Konec cyklu může nastat předčasně, pokud je v těle cyklu obsažen příkaz break nebo return (budeme probírat příště).
Použití iteračního cyklu
Cyklus for používáme vždy, když známe počet opakování určité činnosti.
Iterační cyklus se často využívá pro tvorbu matic (jejichž prvky jsou generovány podle nějakého vzorce) a také je používán při zpracovávání matice prvek po prvku.
Příklad 1 - skript, který vykreslí graf funkce sinus do tří různých grafických oken (není sice příliš praktický, ale pro demonstraci činnosti cyklu si jej vytvoříme):
| sin3krat.m |
% SIN3KRAT - vykresleni grafu sinu do tri grafickych oken x = 0:pi/100:4*pi; % nezavisle promenna for i=1:3 % postupne bude i=1, i=2 a i=3 figure(i) % nove okno (resp. aktivace existujiciho) s cislem 1 nebo 2 nebo 3 plot(x,sin(x),'k') % vykresleni grafu xlabel() % popis osy x ylabel() % popis osy y title() % nazev grafu end |
Doporučení: chcete-li činnost skriptu prozkoumat, krokujte - breakpoint nastavte třeba na řádek x=0:pi/100"4*pi;). Skript spustíte jménem M-souboru bez přípony, tj. >> sin3krat
Příklad 2 - funkce pro výpočet faktoriálu zadaného čísla (na principu: n!=1*2*...*(n-1)*n):
| fakt2.m |
function f=fakt2(n)
% FAKT2 - vypocet faktorialu celeho cisla
% f=fakt2(n)
% n ... cislo
% f ... faktorial (f=n!)if n<0 % kontrola vstupu
error('faktorial neexistuje') % KONEC, nic nepocitame
end
f = 1; % priprava vysledku
for i=1:n % n-krat, anebo: i=2:n (usetrime jedno nasobeni jednickou)
f = f*i; % pridavame do vysledku
end
% nakonec je 'i' rovno 'n' a 'f' obsahuje jeho faktorial 'n'
|
Doporučení: chcete-li činnost funkce prozkoumat, krokujte např. pro >> vysledek=fakt2(5) (breakpoint nastavte třeba na řádek s příkazem if).
Porovnejte funkci fakt2 s funkcí fakt1 - zjistíte podobnost (a rozdíly) mezi oběma druhy cyklů.